[First published: September, 2005]

No one makes bad software on purpose. No programmer has ever sat down, planning out weeks of work, with the intention of frustrating people enough to make them cry. Bad software, or bad anything, happens because making things is hard, making good things doubly so.

The three challenges:

1. Possessing the diverse skills needed to make good things.
2. Understanding who you’re making the thing for.
3. Leading through the chaos of projects with real constraints.

Individually these challenges are significant, but combined they create a wall of probable disappointment high enough few people can see the top, much less the way to the other side.

What it means to say “This sucks”

Whenever you hear someone say “This sucks” they are doing several things simultaneously: expressing frustration, experiencing shock, using criticism to mask feelings of helplessness in a cruel universe, and, most importantly, communicating the gap between their expectations and reality. It’s rare to hear people complain about things they don’t care about.

One way to think about how people respond to things is this spectrum:

• What is this for?
• I have it but haven’t tried it
• I’m annoyed by this, but I don’t need it often
• This Sucks
• This is acceptable
• This is cool / I love it
• This works so well I don’t even think about it

This is just one representation of how people respond to things. The point of this representation is that “this sucks” is right in the middle. In order for people to say “this sucks” they have to care enough about the thing you’ve made to spend time with it and recognize how bad it is. For things that are equally bad, but are unimportant to someone, you won’t hear the same complaint. We’re frustrated most in life by things that come close to our deepest needs, but don’t deliver. It’s the things that tease us, making us think they’ll satisfy us but then fail, than hurt the most.

Looking towards the bottom of the spectrum, the better designed something is the more positive the responses are. But the surprise is that the best possible design for many things, especially things perceived as work, requires no change in behavior for the person using the thing. These designs are so good they eliminate unnecessary interactivity: they just do what they’re supposed to do without bothering you. Think better batteries, tastier food, fuel injection systems, web server upgrades, etc.

For most people, most of the time, they really don’t care about the details of however the thing you’ve made works: they care only about the effects of the thing you made. If they can enjoy most of the benefits without any work, they’ll be very happy.

This suggests that one common reason for suckage is the creator (or programmer) wanting to share their world, the internal world of how things work, with their consumers. They may do this out of love: “If I think this is fun, won’t they?” But often there is a violent mismatch of desires. The creator wants the consumer/user to care about the very things the consumer doesn’t care about.

For example:

Creator: I love the power of Unix/AJAX/C#/whatever.
Customer: I want to finish my work and go play outside.

Sometimes this love is so strong that when a creator hears a “this sucks” or even a “I can’t figure this out” response, they take it as an attack on their beliefs, rather than feedback on the details of the design. Creators, often sensitive about their work, may respond by rejecting the very people they were supposed to be designing for, starting the ugly downward spiral of resentment and passive aggressiveness between creators and consumers, which can end only with one result: software that sucks.

The translation table for “this sucks”

If you look deeper, you’ll find that when people say “this sucks” they mean one or more of the following:

• This doesn’t do what I need
• I can’t figure out how to do what I need
• This is unnecessarily frustrating and complex
• This breaks all the time
• It’s so ugly I want to vomit just so I can see something prettier
• It doesn’t map to my understanding of the universe
• I’m thinking about the tool, instead of my work

These issues represent a diversity of skill failures. To avoid causing these feelings in people you’d need a combination of talents few people have. The above list represents skills including: interaction design, software engineering, quality assurance, product planning/strategy, visual design and project management. Some rare individuals are good at all these things and god bless them, but most of us need to admit and grow out of our weaknesses, or involve other people if we want to make things that don’t suck.

If we invert these feelings, we’ll find common responses people have to good software.

• This satisfies my needs
• I can figure out how to do what I need
• This is smooth, seamless and fun
• This never fails
• It’s beautiful
• It is based on my understanding of the universe
• I think about the results I want, not the tools

These responses never happen by accident. And it’s not brilliance or genius levels of skill that makes it happen either. Instead it’s the orchestration, the combination of different skills that makes it all come together (or not). You might call this direction, leadership, management or some other word. There might be a person who has the dedicated role for it, or it could be a communal responsibility. But however it happens, it defines our first law:

Law #1: If you don’t apply the right skills at the right time, you will make bad things. 

The trap is that this law applies no matter how good you are at any particular skill. At a certain point the best thing you can do to prevent making bad software is to start learning a skill you don’t have instead of improving a skill you’ll already strong in.

The learning curve myth

Some of the issues from the translation table above are often hidden behind the notion of learning curves. The creator will say “No no no: it doesn’t suck. You just have to get used to it” even if it’s a website with moving blinking yellow neon text or a laptop with a keyboard made from damp urine soaked cardboard.

The truth is that human beings can tolerate lots of stupid annoying things: just because your website forces my brain to rewire itself to work around your incompetence doesn’t mean you’ve designed something well. I admit that to make a new thing possible demands change, but how much that change negatively impacts the user is the designer’s burden: they should be protecting me from unnecessary work.

As a first order principle, the best designs require little new learning. The design should meet me where I am and improve my life without me having to do anything new. Three out of every five times someone speaks of a learning curve, they’re just in denial about a weak design.

The definition of a good learning curve has two parts:

1. The design returns value beyond the learning cost paid. If I pay 10 hours of learning time, but get 20% more productivity afterwards, earning me my time back plus more, it’s a good trade.
2. The design matches the learning expectations of the customer/user. I might be willing to suffer an intense two weeks to learn a new language (given my faith in #1), but I’d be upset about investing that much time just to get $50 out of my local bank machine.

Whether the designer realizes it or not they are deciding how much of a learning curve users will experience. Since most of the time most people are using websites, software and other things made by other people, it’s good advice to assume that people don’t want to invest much effort in learning how to use your particular creation. They’d much prefer you reuse the knowledge they’ve already paid the price to learn.

The expectation gap

Expectations are tricky. When we complain about the world we’re really saying that we don’t like how different reality is from what we expected. When someone says “this sucks” they’re really saying “this doesn’t meet my expectations”.

Since every person is different (some more different than others), good designers spend time trying to understand and work to match or exceed people’s expectations. This is a highly speculative activity (there are methods that help, but that’s not my point). People’s expectations change all the time, and the larger the group of people you’re designing for, the greater the probability that some of their expectations will be in conflict. Which gives us the following law:

Law #2: No matter what you do, someone, somewhere will think your software sucks.

This isn’t a justification for bad software. But it is a reminder that every piece of software in the history of the universe (including Apple products) has someone somewhere that hates them. As a rule, the larger the group of people you are trying to design for, the more complex the matrix of expectations you, as a designer/creator, have to manage. It’s for this reason that many market leading products (music, food, clothes) take safe, conventional approaches to how they look and behave: they’re trying to find a sweet spot, however bland, in the expectation matrix of thousands (or millions of) people.

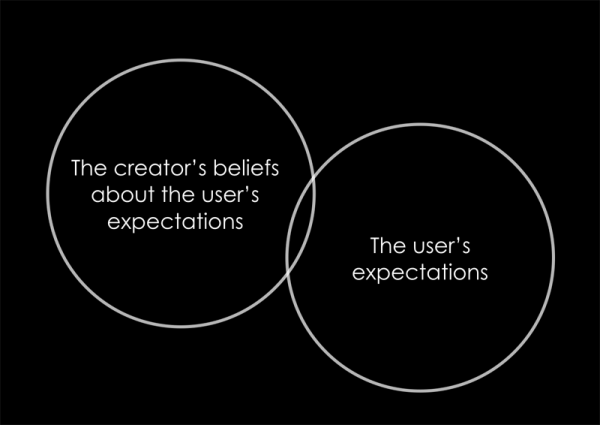
Creators set their own expectations for other people’s expectations. They imagine how other people perceive the world and predict how they’ll respond to the design decisions he makes to please them (There are methods to test/improve these predictions, but that’s not my point either). If the creator is selfish, or is working primarily to satisfy a personal artistic objective, he may deem the world’s expectations irrelevant (e.g. “I code/design/paint for me alone!”). But if he’s trying to help people, or make something for others to use, he’s obligated to generously study their expectations.

Assuming you’re not an artist, the more time you spend defining the specific group(s) of people you are designing for, the easier it will be to make good software. You’ll know, from day one, whose expectations you do not care about. Knowing who you are not designing for is as useful in the design process as knowing who you are designing for. Even if you think you are designing for everyone, there will groups that are more important than others and before you start designing it helps to identify them.

It is possible to influence expectations for something before it’s used. Advertising and branding are two approaches to setting expectations, perhaps unrealistic ones, before people even encounter the designed thing itself. This can lead to trouble: looking at an advertisement can be more satisfying than using the product itself.

How bad things get made

As an exercise, I’m going to describe how to make bad things. Just imagine that for once you were asked to make something really bad that would be so awful people would cry for days after using it (wouldn’t that be fun, just for once?). What would you do? One answer is the following:

• General incompetence: I’d hire the worst people, pay them poorly, give them bad equipment and unpleasant working conditions, and yell at them often.
• Unclear purpose: I’d never explain the goals, never rationalize the non-existent business plan with the non existent product plan, and randomly change my mind about important things every few hours. Once a week, in the morning, I’d act just sane enough to gain people’s confidence, only to obliterate it in the afternoon.
• Unplanned design: I’d wait as long as possible to think about what the customer’s experience should be, so that decisions that most impact the people I’m designing for have the fewest resources, the most constraints and the lowest possible probability of a quality outcome.
• Poor engineering: I’d demand people build things that frequently fail in dramatic, surprising and dangerous ways.
• Make customers miserable: Our only team motto will be “They must suffer more”. We’d watch the Monty Python Spanish Inquisition scene to master all of our chief weapons, ensuring maximum suffering for every customer we have.

If this sounds like your team, you should read how to survive a bad manager and how to learn from your mistakes.

Jokes aside, all projects have problems. No team, leader or programmer is perfect. None of us are are omnipotent (despite our egos) nor are we immune from mistakes and oversights. Even if you have good people, decent resources and a reasonable plan, keeping things together and on track every day is amazingly hard. There are always variables out of your control, the politics of powerful people, miscommunications, unavoidable complications, frustrating setbacks, disruptive competitors and bureaucratic firestorms. Goodness is fragile: even if you get most of it right the bits you miss can spoil everything. To make good things is much more difficult than simply having good ideas or good skills.

But there’s a deeper problem. Even before the work begins, everyone has underlying, and different, ideas of what the important work is. To truly understand bad software, we have to talk about two different beliefs about how things are made.

Construction vs. Design

Good architects, the people who make good buildings, are taught the difference between construction and design. Design is a process that explores different perspectives on the work, business, engineering, aesthetics, customers, the environment and integrates them into a plan, or a direction for a plan. Design starts with big strokes: sketches and prototypes for the customer’s experience that take on the big questions about the work (What’s it for? Who’s it for? How might it work? How will we know it’s successful?).

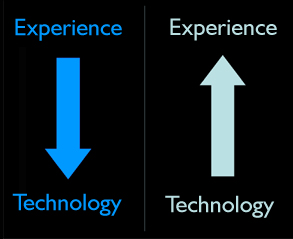Construction is the act of building things with technology. Things are created, put into a specific order or combination, with respect for reliability, performance, safety and security. It starts with small pieces and puts them together to make bigger pieces.

A design centric mindset starts by figuring out the experience and after it has some shape, available technologies are used to make that experience real. A construction centric mindset starts with the technologies first and figures out the desired experience later on.

Software, made from bits which are entirely more flexible than atoms, blends together construction and design giving one person enormous power to make things. But the risk of that power is that they will emphasize the personal immediacy of construction (“I’m making something!”) over the poise and wisdom need to make good things (“I’m thinking deeply about how this will be used, and who will use it, before I start construction”).

Nothing prevents a programmer from switching back and forth between construction and design. But in many cases there’s nothing that motivates them to do it either. Without design, construction can go wherever it pleases, without regard for anyone but the creator. The result is often a mismatch: software that is heavily built with a construction heavy aesthetic, like a cold military bunker, while the consumer needed something like a cute vacation cabin suitable for cozy weekend trysts.

Beautiful code, computer science and other loves

One illustration of the philosophical differences between love of construction and love of good things is the belief that code should be beautiful. I’m a fan of beautiful things: the world can use more of them, including more lines of beautiful code. But the trap is that code is an artifact of constructing software. When code is well written (beautiful or homely), it compiles. And it’s the output of the compiler (or browser) that people see. It’s the complied code that changes the world. The beauty of the code is relevant only to people that look at code. To worry about code aesthetics more than the aesthetics of the product itself is akin to a song writer worrying about the aesthetics of the sheet music instead of the quality of the sounds people hear when the band actually plays.

It suggests a love of construction (and for others doing construction), more so than a love of how construction effects people in the world. Both kinds of love are good, but there are important difference between them, especially when talking about how to make good things. You need a balance of both kinds if you want to make everyone, the creator and the customer, happy.

Computer science is taught with a construction mentality. Even the theory and philosophy that are covered support construction, not higher level design, or how to make good software in the sense I’ve described. Aspects of design are covered, but at an internal level, the design of object models, data structures and networks, not at the level of what happens when the technology meets the world or the people in it (often called Human computer interaction, ui design, or interaction design). The trend is getting better, some schools do at least offer HCI courses as electives, but that’s only one piece of the suck puzzle.

Graduating with a degree in Computer science does not prevent you from making software that sucks. In fact it might increase the odds of suckage, since it gives you powerful skills to make something, but little understanding of how many factors contribute to making something good. A specialized degree gives you little awareness of the skills you don’t have.

How good things are made

When you create you are exercising the greatest power in the universe: bringing something that didn’t exist before into the world. Making something for others is a gift. Few people in the world have the privilege of earning a living by creating things. If you build things for yourself, you are both the creator and the consumer. But if you are making things for others, you don’t receive the gift: you are the gift giver.

Most people suck at giving gifts (even to themselves: most of us don’t even know how to make ourselves happy, much less others). We could all fill rooms with the lifetime of junk we’ve received as gifts from people that: were careless, thoughtless, insincere, cheap, indifferent to or ignorant of our needs, had bad taste, no skills, or simply didn’t know us well enough to give something we’d enjoy. Bad software is a bad gift. All of the failures that lead to bad gifts apply to bad software.

Good things in the world come from people that have the gift mentality. They do care about who they are designing for. They are sincere about trying to build something that will satisfy a person’s needs. They are willing to expend time and energy refining their thinking and developing new skills so that when they are finished they can sincerely offer what they’ve made to the world as a good thing. They see their work as a deep expression of generosity and as an attempt to live up to their own ideal of quality and workmanship.

Good programmers, designers, architects or creators of any kind are simply thoughtful. They are so passionate about making good things, that they will study any discipline, read any book, listen to any person and learn any skill that might improve their abilities to make things worthy of the world. They tear down boundaries of discipline, domain or job title, clawing at any idea, regardless of its origins, that might help them make a better thing.

What to do about all this

The flippant response among design and usability professionals, as well as programmers, testers, and businessmen, is that they should be more involved (or have more power). Sometimes this is true, sometimes not. Law #1 tells us it’s the right skill at the right time, not one skill all the time. Having experts in design/usability/whatever in the room helps, but if no one listens to them, or if no one listens to anyone else, you will have bad software on your hands.

Instead the burden, as always, falls to the leaders, and anyone who feels they need more power should consider taking on a generalized leadership role, rather than a specialized expert role. It’s up to leaders and managers to decide which skills are important and to figure out when and how to use them. For programmers working alone, they are the leader. For teams or entire organizations, there are probably several leaders who collectively define what matters and what doesn’t. At the end of the day it’s up to them to get the right people in the room and to focus their energy in the right way.

There’s certainly more to be said about making good things, but that’s nearly all I can fit in this essay beyond what I’ve already said.

Looking at good things

Good things are easy to miss. They don’t scream for your attention or chase you the way advertising for mediocre things often does. You have to cultivate the skill in finding good things, and pay attention to those around you that have a knack for finding them.

But we, as consumers (particularly Americans), are so buried in things made for us by others that we’ve fallen into an arrogant attitude. We forget that behind every song, automobile, movie, or website was at least one person that slaved for months or years to make what we see. The fact we think something is bad doesn’t mean the work done to make it isn’t worthy of respect. Often even mediocre things have good stories of triumph and creativity behind them that we can learn from.

To understand good, or even great things, we have to turn our consumer instincts off, and think like creators. Whenever I see something that’s good, or even something that’s bad in an interesting way, after I’ve used it and looked at it, I ask the following questions:

• How did they do this?
• How much time did it take them? What techniques did they use? How many people were involved?
• How did they engineer it to achieve the effects it has?
• What training did they have?
• How much of the engineering is even visible when I use it?
• What makes it so good? Why can’t I stop looking at it, using it, sleeping with it, or rubbing it all over my body?
• How did it work so well that it did so much for me without me even thinking about it?
• What were they trying to do? Were they happy with the result? How do they see it?
• How would I have made something like this?
• What other creators do I know and how do they respond to this thing?
• How does the rest of the world respond to this thing? Why is their response different than mine?

It takes enormous craft, discipline and experience to make something good. The masters in any field tend to be the ones who work both harder and smarter than others, and are more willing to try out new ideas and consider other peoples opinions. In examining how other good things are made, I’m sure you’ll return to your own work with a broader perspective. You’ll have new ideas and will ask new questions about your habits, biases and attitudes that you didn’t think to ask before. you didn’t before.

To get you started, here’s some good things I’ve looked at, but you should really find your own:

References & Notes

This essay is a recasting of what I’ve learned over a career. It was presented at O’Reilly Media’s FOO Camp 2005 (thanks to those that came). Many of the same core ideas are expressed for a wide audience in my book How Design Makes The World.

I did not refer directly to books or sources in writing this essay, but several come to mind as references.

• The design of everyday things, Don Norman. This is most well known UI design and human factors book in the world. It serves as a fantastic introduction to thinking about the mental processes people use to interact with the world and breaks down why many objects are so prone to causing frustration. It’s well written and filled with pictures. But it does not offer a solution or a process for avoiding failure.
• The elements of friendly software design, Paul Heckel. This is an amazing little book. It’s the perfect companion to design of everyday things, since it focuses on how to approach things from the creator’s view, not the analysts view. It’s a hidden gem – few people know of this book (Steve Capps is the only designer I’ve met that had even heard of it).
• Why ease of use doesn’t happen. This is a short catalog of specific organizational and team failures that make ease of use impossible.
• Flow, By Mihaly Csikszentmihalyi . Here is the best reading about what’s going on when you get lost in your work or play. Good software has the same effect, helping people get lost in the experience instead of struggling with the tools.
• Digital Woes: Why we should not depend on software, Lauren Weiner. A well written collection of stories about why software failures, of various kinds, are inevitable. Written for a lay audience and a better read that other similar books I’ve read.
• The inmates are running the asylum, By Alan Cooper. Be warned: this is a well written but strongly opinionated piece. It excels at capturing many of the underlying reasons bad things are made, breaking down how technologists and businessmen can allow their biases to get in the way. The problem is that few practical remedies are offered here. Cooper also tends to blame programmers for just about everything, but the strengths of his points and his writing earns it a place here.

Here are some other related writings:

• Why software is so bad, MIT Technology review
• Why software sucks, Libretti
• Why software sucks, Byte (registration)
• All hardware sucks, all software sucks, The Jargon File (ESR)
• Why software stiil sucks, Jaron Lanier interview
• Software disasters, MSNBC
• Software: so bad it can only get better (1996), Computerworld
• Why is software so bad, Edward Tufte et. al.
• If there’s a canonical reference I don’t have for this rantish topic, let me know.

[First published September, 2005]